Sequência Recursiva: Propriedades E Exemplos Com Exercícios Resolvidos – embarque nesta jornada fascinante pelo mundo das sequências recursivas! Desvendaremos os mistérios por trás desses padrões matemáticos elegantes, explorando suas propriedades intrínsecas e a beleza da sua definição recursiva. Prepare-se para mergulhar em exemplos práticos e exercícios resolvidos que iluminarão o caminho para uma compreensão profunda deste conceito fundamental da matemática, revelando a elegância e a potência da recorrência na resolução de problemas complexos.
A cada passo, desvendará novos insights, construindo uma sólida base para futuras explorações matemáticas.
De sequências aritméticas e geométricas a padrões mais complexos, como a sequência de Fibonacci, exploraremos a riqueza e a diversidade das sequências recursivas. Aprenderemos a identificar suas características únicas, a distinguir a recorrência da iteração e a dominar a arte de construir e interpretar definições recursivas, incluindo a crucial condição de parada. Através de exemplos cuidadosamente selecionados e exercícios passo a passo, você construirá confiança e proficiência na manipulação e resolução de problemas envolvendo sequências recursivas, abrindo portas para um mundo de possibilidades matemáticas.
Conceito e Definição de Sequência Recursiva
Embarque conosco numa jornada fascinante pelo mundo das sequências recursivas, estruturas matemáticas que revelam uma elegância intrínseca e uma capacidade surpreendente de descrever padrões complexos da natureza e da tecnologia. A beleza da recursão reside na sua capacidade de definir um elemento em termos dos elementos que o precedem, criando uma cascata de definições que se auto-sustentam, como um rio que se alimenta das suas próprias nascentes.Uma sequência recursiva é definida por uma relação de recorrência, uma fórmula que expressa cada termo da sequência como uma função de um ou mais termos anteriores.
Esta definição, ao contrário de uma fórmula explícita que calcula diretamente um termo qualquer, se apoia em si mesma, construindo o todo a partir de suas partes. Imagine uma teia de aranha, onde cada fio se conecta a outros, formando uma estrutura complexa e interdependente; a recursão opera de maneira similar, criando uma estrutura matemática a partir de relações entre seus elementos.
A definição completa requer, além da relação de recorrência, a especificação de um ou mais termos iniciais, os quais servem como base para a construção da sequência. Sem esses termos iniciais, a recursão fica sem um ponto de partida, como um navio sem bússola, perdido no mar da abstração.
Diferença entre Recorrência e Iteração na Definição de Sequências
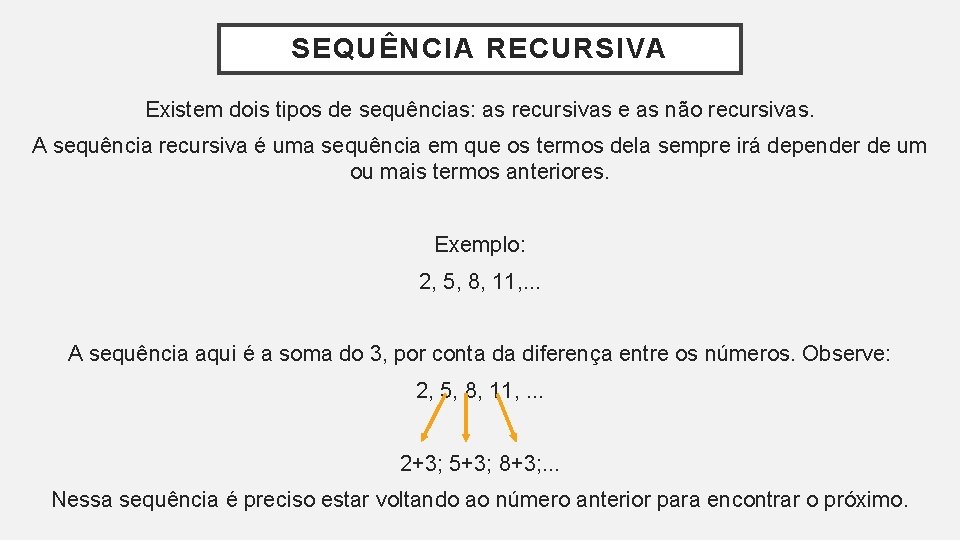
A recorrência e a iteração representam duas abordagens distintas para definir e calcular sequências. A recorrência, como já vimos, define um termo em função de termos anteriores, criando uma definição auto-referencial. A iteração, por outro lado, é um processo que calcula os termos sequencialmente, aplicando repetidamente uma mesma operação a um valor inicial. Imagine a construção de uma pirâmide: a recorrência seria como definir cada bloco em função dos blocos abaixo, enquanto a iteração seria como adicionar um bloco de cada vez, seguindo uma sequência pré-determinada.
A recorrência, em sua essência, é uma definição elegante e concisa, mas a sua implementação pode ser computacionalmente mais complexa do que a iteração, especialmente para sequências extensas. A iteração, embora possa ser mais direta em alguns casos, pode ser menos intuitiva para descrever padrões complexos inerentes à sequência.
Importância da Condição de Parada em uma Definição Recursiva, Sequência Recursiva: Propriedades E Exemplos Com Exercícios Resolvidos
A condição de parada, também conhecida como caso base, é o elemento crucial que impede que uma definição recursiva entre em um loop infinito. Ela é o ponto final da cascata de definições, o ponto em que a recursão se interrompe e o resultado final é obtido. Sem a condição de parada, a recursão continuaria indefinidamente, como um corredor sem linha de chegada, consumindo recursos computacionais e levando a um erro de estouro de pilha.
A condição de parada define o ponto em que o processo recursivo se torna auto-suficiente, retornando um valor calculado diretamente, sem depender de outros termos da sequência. É a âncora que garante a estabilidade e a finalização do processo.
Exemplos de Sequências Recursivas
A tabela a seguir ilustra alguns exemplos de sequências recursivas, incluindo casos especiais como sequências aritméticas e geométricas, destacando suas fórmulas recursivas e explícitas. A fórmula recursiva define o termo n-ésimo em função de termos anteriores, enquanto a fórmula explícita calcula diretamente o termo n-ésimo, sem a necessidade de calcular os termos precedentes.
| Tipo de Sequência | Fórmula Recursiva | Fórmula Explícita | Exemplo |
|---|---|---|---|
| Sequência Aritmética | an = an-1 + r (com a1 = a) | an = a + (n-1)r | 2, 5, 8, 11, … (a=2, r=3) |
| Sequência Geométrica | an = an-1
|
an = a – q n-1 | 3, 6, 12, 24, … (a=3, q=2) |
| Sequência de Fibonacci | Fn = F n-1 + F n-2 (com F 1 = 1, F 2 = 1) | Fn = [φ n
|
1, 1, 2, 3, 5, 8, … |
| Sequência de números de Catalan | Cn = Σ n-1k=0 (C k
|
Cn = (2n)! / [(n+1)!n!] | 1, 1, 2, 5, 14, 42, … |
Propriedades e Características de Sequências Recursivas
Embarque conosco numa jornada fascinante pelo mundo das sequências recursivas! A beleza dessas sequências reside na sua capacidade de se auto-definirem, criando padrões elegantes e complexos a partir de regras simples e repetitivas. Vamos desvendar as propriedades que governam seu comportamento e explorar a riqueza de exemplos que ilustram sua presença na matemática e além.
As sequências recursivas, como um rio que serpenteia, moldam seu curso através de relações intrínsecas entre seus termos. Cada termo é definido em função de termos anteriores, criando uma cascata de dependências que gera padrões surpreendentes. Essa interdependência é a chave para compreender seu comportamento e permite que exploremos suas propriedades fundamentais.
Tipos de Sequências Recursivas e Exemplos
A diversidade das sequências recursivas é vasta, como um jardim repleto de flores únicas. Podemos classificá-las de diferentes maneiras, considerando a natureza das relações entre seus termos. Algumas são lineares, outras não lineares; algumas são homogêneas, outras não. A classificação ajuda a organizar e compreender a riqueza de possibilidades.
-
Sequências Recursivas Lineares de Primeira Ordem: São definidas por uma relação da forma an = c*a n-1 + d , onde c e d são constantes. Um exemplo clássico é a sequência aritmética, onde c=1 e d é a razão comum. Por exemplo, a sequência 2, 5, 8, 11… é definida por an = a n-1 + 3 , com a1 = 2 .
-
Sequências Recursivas Lineares de Segunda Ordem: Aqui, cada termo depende dos dois termos precedentes. A famosa sequência de Fibonacci é um exemplo notável: an = a n-1 + a n-2, com a1 = 1 e a2 = 1 , gerando a sequência 1, 1, 2, 3, 5, 8…
-
Sequências Recursivas Não Lineares: Neste caso, a relação entre os termos não é linear. Um exemplo seria uma sequência onde cada termo é o quadrado do termo anterior: an = (a n-1) 2. Se a1 = 2 , a sequência seria 2, 4, 16, 256…
Propriedades Matemáticas Chave

As sequências recursivas, apesar de sua diversidade, compartilham propriedades matemáticas que as unem e permitem sua análise. Compreender essas propriedades é fundamental para manipular e prever o comportamento dessas sequências.
Uma propriedade crucial é a condição inicial. Sem ela, a sequência não pode ser definida completamente. A condição inicial, ou conjunto de condições iniciais, fornece o ponto de partida para a geração dos termos subsequentes. Outra característica importante é a relação de recorrência, que define a regra que relaciona cada termo aos seus precedentes. Essa relação, em sua essência, é o coração da sequência recursiva, determinando seu padrão e crescimento.
Determinação da Natureza Recursiva de uma Sequência
Nem toda sequência é recursiva. A capacidade de expressar cada termo em função de termos anteriores é o critério fundamental para determinar sua natureza recursiva. Se for possível encontrar uma fórmula que defina essa relação, então a sequência é recursiva.
Consideremos a sequência 1, 4, 9, 16, 25… Cada termo é o quadrado do seu índice (n²). Podemos expressar isso recursivamente como an = a n-1 + 2n – 1 , com a1 = 1 . A existência dessa relação recursiva confirma a natureza recursiva da sequência. Em contraponto, uma sequência como 1, 2, 4, 7, 11…
(onde a diferença entre termos consecutivos aumenta em 1 a cada passo) apresenta um padrão, mas sua expressão recursiva não é trivial, podendo até não existir uma expressão fechada simples.
Exemplos e Exercícios Resolvidos de Sequências Recursivas: Sequência Recursiva: Propriedades E Exemplos Com Exercícios Resolvidos

A beleza da recursão reside na sua elegância e poder. Com poucos comandos, podemos descrever processos complexos, que se repetem de forma organizada e previsível. Nesta seção, mergulharemos em exemplos práticos, desvendando o mistério por trás da aplicação de sequências recursivas em problemas do dia a dia e em desafios matemáticos. Veremos como a definição de um caso base e a relação de recorrência nos levam a soluções elegantes e eficientes.
Exemplos de Problemas Resolvidos Usando Sequências Recursivas

A capacidade de resolver problemas usando recursão se estende a diversas áreas, desde a computação à matemática financeira. Observemos três exemplos distintos que ilustram a versatilidade desse método.
- Cálculo do Fatorial: O fatorial de um número inteiro positivo n (denotado por n!) é o produto de todos os inteiros positivos menores ou iguais a n. A definição recursiva é: n! = n
(n-1)!, com o caso base 0! = 1. Para calcular 5!, por exemplo, podemos aplicar a definição recursivamente
5! = 5
- 4! = 5
- 4
- 3! = 5
- 4
- 3
- 2! = 5
- 4
- 3
- 2
- 1! = 5
- 4
- 3
- 2
- 1 = 120. Cada etapa reduz o problema a um caso menor, até atingir o caso base.
- Torre de Hanói: Este famoso quebra-cabeça consiste em mover uma pilha de discos de uma haste para outra, usando uma haste auxiliar, respeitando as regras: mover apenas um disco por vez, nunca colocar um disco maior sobre um menor. A solução recursiva é elegante: para mover n discos da haste A para a haste C, primeiro movemos n-1 discos de A para B (recursivamente), então movemos o maior disco de A para C, e finalmente movemos os n-1 discos de B para C (recursivamente).
O caso base é quando temos apenas um disco ( n=1).
- Busca em Árvore: Em ciência da computação, a busca por um elemento em uma árvore de busca binária pode ser feita recursivamente. A ideia é comparar o elemento buscado com a raiz da árvore. Se o elemento for igual à raiz, a busca termina. Se for menor, a busca continua na subárvore esquerda; se for maior, na subárvore direita. O caso base é quando a subárvore a ser pesquisada é vazia (elemento não encontrado).
Exercício Resolvido: Sequência de Fibonacci

A sequência de Fibonacci é definida recursivamente por F(n) = F(n-1) + F(n-2), com os casos base F(0) = 0 e F(1) = 1. Vamos calcular o 6º termo da sequência (F(6)).
- F(0) = 0
- F(1) = 1
- F(2) = F(1) + F(0) = 1 + 0 = 1
- F(3) = F(2) + F(1) = 1 + 1 = 2
- F(4) = F(3) + F(2) = 2 + 1 = 3
- F(5) = F(4) + F(3) = 3 + 2 = 5
- F(6) = F(5) + F(4) = 5 + 3 = 8
Portanto, o 6º termo da sequência de Fibonacci é 8.
Exercício Resolvido: Identificação do Termo Geral
Dada a sequência recursiva definida por an = 2a n-1 + 1 , com a1 = 1 , encontre o termo geral an.
Vamos seguir os passos para encontrar o termo geral:
| Passo | Descrição do Passo |
|---|---|
| 1 | Calcular os primeiros termos da sequência: a1 = 1, a2 = 2(1) + 1 = 3, a3 = 2(3) + 1 = 7, a4 = 2(7) + 1 = 15, a5 = 2(15) + 1 = 31… |
| 2 | Observar um padrão: Os termos parecem ser da forma 2n – 1. |
| 3 | Testar a hipótese: Para n=1, 21
|
| 4 | Demonstrar por indução: Base: a1 = 211 =
1. Hipótese indutiva Assumimos que a k = 2 k
|
| 5 | Conclusão: O termo geral da sequência é an = 2n – 1. |

