O Que São Numeros Irracionais Exemplos – O Que São Números Irracionais: Exemplos e Aplicações mergulha no fascinante mundo dos números que desafiam a representação como frações simples. Explore a natureza única desses números, que se estendem infinitamente sem padrões repetitivos, e descubra como eles impactam áreas como geometria, física e muito mais.
Números irracionais, como π (pi) e √2 (raiz quadrada de 2), são frequentemente encontrados em situações do dia a dia, mesmo que não percebamos. Ao explorarmos a relação entre o perímetro e o diâmetro de um círculo, por exemplo, encontramos π, um número irracional que representa a constante fundamental da geometria.
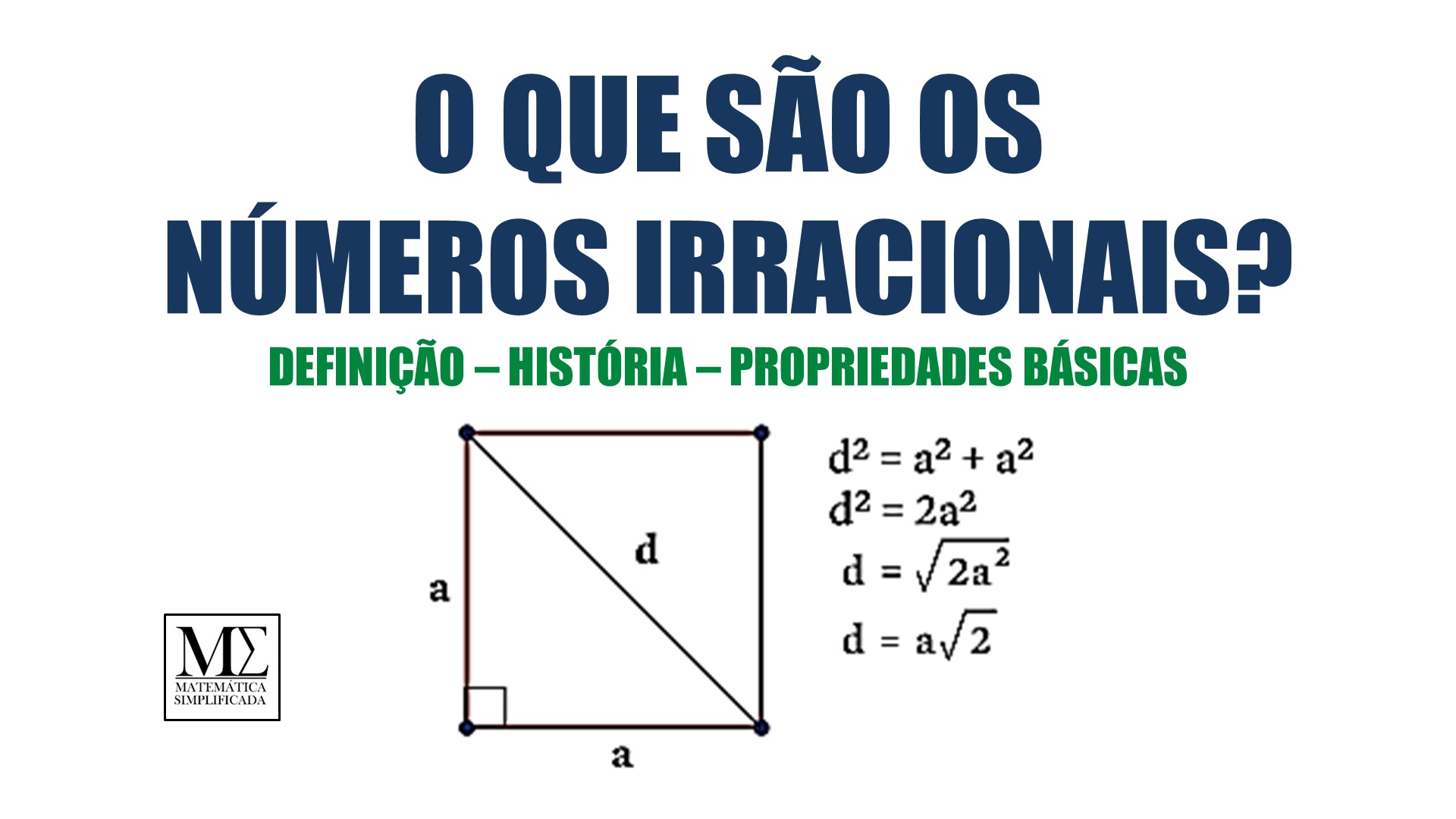
Da mesma forma, a diagonal de um quadrado, expressa como √2, é outro exemplo de número irracional que aparece em aplicações práticas.
Introdução aos Números Irracionais: O Que São Numeros Irracionais Exemplos
Números irracionais são um tipo especial de número que não pode ser expresso como uma fração de dois inteiros. Em outras palavras, eles não podem ser escritos na forma a/b, onde a e b são inteiros e b não é zero.
Esses números têm propriedades únicas que os distinguem dos números racionais, e desempenham um papel crucial em vários campos da matemática e outras áreas da ciência.
Definindo Números Irracionais
A principal característica que define um número irracional é sua incapacidade de ser expresso como uma fração de dois inteiros. Por exemplo, o número pi (π), que representa a razão entre a circunferência de um círculo e seu diâmetro, é um número irracional.
Ele não pode ser escrito como uma fração simples, embora sua aproximação seja frequentemente usada como 22/7. Outro exemplo clássico é a raiz quadrada de 2 (√2), que representa o comprimento da diagonal de um quadrado com lados de comprimento 1.
√2 também não pode ser expresso como uma fração simples.
Diferença entre Números Racionais e Irracionais
A principal diferença entre números racionais e irracionais reside na capacidade de serem representados como frações. Números racionais, como 1/2, 3/4 ou 5, podem ser expressos como uma fração de dois inteiros. Por outro lado, números irracionais, como π e √2, não podem ser expressos dessa forma.
Essa diferença fundamental tem implicações importantes na forma como esses números são manipulados e usados em cálculos matemáticos.
Propriedades dos Números Irracionais
Os números irracionais possuem propriedades únicas que os distinguem dos números racionais. Essas propriedades são derivadas da natureza infinita e não periódica de sua representação decimal.
Representação Decimal Infinita e Não Periódica
Uma característica crucial dos números irracionais é que sua representação decimal é infinita e não periódica. Isso significa que os dígitos após o ponto decimal continuam para sempre e não formam um padrão repetitivo. Por exemplo, o número pi (π) tem uma representação decimal infinita e não periódica: 3,14159265358979323846…
Os dígitos continuam infinitamente sem qualquer padrão repetitivo. Da mesma forma, a raiz quadrada de 2 (√2) também tem uma representação decimal infinita e não periódica: 1,41421356237309504880… A natureza infinita e não periódica da representação decimal é uma propriedade fundamental que distingue os números irracionais dos números racionais.
Comparando Propriedades com Números Racionais
As propriedades dos números irracionais contrastam fortemente com as dos números racionais. Números racionais podem ser expressos como uma fração de dois inteiros, e sua representação decimal é finita ou periódica. Por exemplo, 1/2 tem uma representação decimal finita (0,5), enquanto 1/3 tem uma representação decimal periódica (0,333…).
Os números irracionais, por outro lado, não podem ser expressos como frações e sua representação decimal é infinita e não periódica. Essa diferença fundamental torna os números irracionais únicos e importantes em matemática.
Importância dos Números Irracionais
Os números irracionais desempenham um papel crucial em vários campos da matemática e outras áreas da ciência. Eles são essenciais para entender e descrever conceitos geométricos, como a relação entre a circunferência e o diâmetro de um círculo (π), ou a diagonal de um quadrado (√2).
Os números irracionais também são usados em trigonometria, cálculo e física, onde são essenciais para modelar e resolver problemas complexos. A importância dos números irracionais está relacionada à sua capacidade de representar quantidades que não podem ser expressas como frações simples, expandindo o escopo da matemática e abrindo caminho para novos entendimentos e aplicações.
Exemplos de Números Irracionais
Existem muitos exemplos de números irracionais além de π e √2. Esses números podem ser encontrados em diferentes áreas da matemática e da ciência, e são usados para representar quantidades que não podem ser expressas como frações simples.
Tabela de Tipos e Exemplos
| Tipo de Número Irracional | Exemplo 1 | Exemplo 2 | Exemplo 3 |
|---|---|---|---|
| Raízes quadradas de números não quadrados perfeitos | √3 | √5 | √7 |
| Raízes cúbicas de números não cubos perfeitos | ∛2 | ∛5 | ∛7 |
| Números transcendentais | e | ln(2) | φ (número de ouro) |
| Constante de Euler-Mascheroni | γ | – | – |
Números Irracionais em Contextos Reais
Os números irracionais são encontrados em muitos contextos reais. Por exemplo, a relação entre a circunferência de um círculo e seu diâmetro é representada pelo número irracional π. Isso significa que a circunferência de um círculo é sempre π vezes o diâmetro.
Outro exemplo é a diagonal de um quadrado, que é √2 vezes o comprimento de um lado do quadrado. Esses exemplos demonstram como os números irracionais estão intrinsecamente relacionados a formas geométricas e padrões no mundo real.
Aplicações dos Números Irracionais
Os números irracionais têm uma ampla gama de aplicações em diferentes áreas da matemática, ciência e engenharia. Eles são ferramentas essenciais para resolver problemas complexos e modelar fenômenos naturais.
Geometria e Trigonometria
Em geometria, os números irracionais são usados para calcular áreas, volumes e perímetros de formas geométricas. Por exemplo, a área de um círculo é calculada usando a fórmula A = πr², onde r é o raio do círculo. O número irracional π é essencial para calcular a área de qualquer círculo.
Em trigonometria, os números irracionais são usados para calcular os valores de funções trigonométricas, como seno, cosseno e tangente. Por exemplo, o seno de 30 graus é √3/2, que é um número irracional.
Cálculo e Física

No cálculo, os números irracionais são usados para representar limites, derivadas e integrais. Por exemplo, o limite de 1/x quando x se aproxima de 0 é infinito, que é um número irracional. Em física, os números irracionais são usados para modelar fenômenos como o movimento de um pêndulo, a propagação de ondas e o comportamento de partículas subatômicas.
Por exemplo, a constante de Planck, que é uma constante fundamental na física quântica, é um número irracional.
Engenharia e Outros Campos
Os números irracionais também são usados em engenharia, computação, economia e outras áreas. Por exemplo, em engenharia, os números irracionais são usados para calcular a resistência de materiais, a frequência de ondas eletromagnéticas e o comportamento de sistemas dinâmicos. Em computação, os números irracionais são usados para gerar números aleatórios e para desenvolver algoritmos de criptografia.
A aplicação dos números irracionais é vasta e continua a expandir à medida que novas descobertas e tecnologias surgem.
FAQs
Como posso identificar um número irracional?
Um número irracional não pode ser expresso como uma fração de dois inteiros. Sua representação decimal é infinita e não periódica.
Quais são alguns exemplos de números irracionais além de π e √2?
Outros exemplos incluem o número de Euler (e), a raiz cúbica de 3 (∛3) e o número áureo (φ).
Por que os números irracionais são importantes?
Os números irracionais são essenciais para a precisão em cálculos matemáticos e científicos, especialmente em áreas como geometria, física e engenharia.

