Exemplo De Função Do 2 Grau Exercicios Resolvidos Com Graficos! Prepare-se para uma jornada fascinante pelo mundo das funções quadráticas! Vamos desvendar os segredos por trás dessas curvas encantadoras, explorando desde a equação geral até a construção precisa de seus gráficos. Dominaremos técnicas poderosas como a fórmula de Bhaskara e a fatoração, desvendando raízes, vértices e concavidades com maestria.
Prepare-se para visualizar a matemática em ação, com exemplos práticos que vão te surpreender!
Neste guia completo, você encontrará exercícios resolvidos passo a passo, tabelas ilustrativas e explicações claras e concisas. Descobriremos como as funções do segundo grau se aplicam a situações reais, mostrando sua importância em diversas áreas do conhecimento. Aprenderá a interpretar gráficos, prever comportamentos e resolver problemas com confiança e precisão. Prepare-se para se tornar um expert em funções quadráticas!
Introdução à Função do 2º Grau: Exemplo De Função Do 2 Grau Exercicios Resolvidos Com Graficos
A função do 2º grau, também conhecida como função quadrática, é uma função polinomial de grau 2 que desempenha um papel crucial em diversas áreas da matemática e suas aplicações. Sua representação gráfica é uma parábola, uma curva com características geométricas específicas que permitem a análise de seus comportamentos e soluções.
Forma Geral da Equação Quadrática
A forma geral da equação de uma função quadrática é dada por: f(x) = ax² + bx + c, onde a, b, e c são coeficientes reais, e a é diferente de zero (a ≠ 0). A condição a ≠ 0 garante que a função seja de fato quadrática.
Significado dos Coeficientes a, b e c
Os coeficientes a, b, e c influenciam diretamente a forma e a posição da parábola no plano cartesiano. O coeficiente a determina a concavidade da parábola (para cima se a > 0, para baixo se a < 0) e o seu "fechamento" (quanto maior o valor absoluto de a, mais fechada a parábola). O coeficiente b afeta a posição do vértice da parábola e sua inclinação.
O coeficiente c representa o ponto de interseção da parábola com o eixo y (o valor de f(x) quando x = 0).
Representação Gráfica: A Parábola
A representação gráfica de uma função do 2º grau é uma parábola, uma curva simétrica em relação a uma reta vertical chamada eixo de simetria. O ponto onde a parábola intercepta o eixo de simetria é o vértice da parábola, que representa o ponto de máximo ou mínimo da função, dependendo da concavidade.
Exemplos de Funções do 2º Grau e suas Parábolas
| Função | Coeficiente a | Coeficiente b | Descrição da Parábola |
|---|---|---|---|
| f(x) = x² + 2x + 1 | 1 | 2 | Parábola com concavidade para cima, vértice em (-1, 0), interceptando o eixo y em (0, 1). É uma parábola “aberta”, com concavidade relativamente suave. |
| f(x) = -2x² + 4x – 2 | -2 | 4 | Parábola com concavidade para baixo, vértice em (1, 0), interceptando o eixo y em (0, -2). É uma parábola mais “fechada” que o exemplo anterior, devido ao valor de ‘a’. |
| f(x) = 0.5x² – 3 | 0.5 | 0 | Parábola com concavidade para cima, vértice em (0, -3), interceptando o eixo y em (0, -3). Parábola mais aberta que o primeiro exemplo, devido ao valor menor de ‘a’. |
| f(x) = -x² + 1 | -1 | 0 | Parábola com concavidade para baixo, vértice em (0, 1), interceptando o eixo y em (0, 1). Concavidade semelhante ao segundo exemplo, porém com vértice diferente. |
Encontrando as Raízes (Zeros) da Função
As raízes, ou zeros, de uma função do 2º grau são os valores de x para os quais f(x) = 0. Esses valores representam os pontos de interseção da parábola com o eixo x. Existem dois métodos principais para encontrar as raízes: a fórmula de Bhaskara e a fatoração.
Métodos para Encontrar as Raízes
A fórmula de Bhaskara e a fatoração são métodos eficazes para determinar as raízes de uma equação quadrática. A escolha do método depende da estrutura da equação e da facilidade de aplicação em cada caso.
Comparação entre Fórmula de Bhaskara e Fatoração
A fórmula de Bhaskara é um método geral que sempre fornece as raízes, mesmo quando a equação não pode ser fatorada facilmente. A fatoração, por sua vez, é mais rápida quando aplicável, oferecendo uma solução mais direta. A fórmula de Bhaskara, porém, pode envolver cálculos mais complexos, especialmente com coeficientes não inteiros.
Resolução de Exercícios Utilizando a Fórmula de Bhaskara
Vamos resolver três exemplos utilizando a fórmula de Bhaskara: x = (-b ± √(b²
-4ac)) / 2a
- Exemplo 1: f(x) = x²5x + 6. a = 1, b = -5, c = 6. Aplicando a fórmula, encontramos x = 2 e x = 3.
- Exemplo 2: f(x) = 2x² + 4x – 6. a = 2, b = 4, c = -6. Aplicando a fórmula, encontramos x = 1 e x = -3.
- Exemplo 3: f(x) = x²4x + 4. a = 1, b = -4, c = 4. Aplicando a fórmula, encontramos x = 2 (raiz dupla).
Resolução de Exercício Utilizando Fatoração
Vamos resolver um exemplo utilizando a fatoração:
Exemplo: f(x) = x²
-7x + 12
- Encontrar dois números que multiplicados resultem em 12 e somados resultem em -7. Esses números são -3 e -4.
- Reescrever a equação como: (x – 3)(x – 4) = 0
- Resolver as equações: x – 3 = 0 => x = 3; e x – 4 = 0 => x = 4.
- Portanto, as raízes são x = 3 e x = 4.
Vértice da Parábola
O vértice da parábola é o ponto de máximo ou mínimo da função, dependendo da concavidade. Suas coordenadas, (x v, y v), são importantes para o esboço do gráfico da função.
Cálculo das Coordenadas do Vértice
As coordenadas do vértice podem ser calculadas usando as seguintes fórmulas:
xv = -b / 2a
yv = f(x v) = a(x v)² + b(x v) + c
Encontrando o Vértice com Exemplos Numéricos
Vamos encontrar o vértice de três funções:
- f(x) = x² + 2x + 1: xv = -2 / (21) = -1; y v = (-1)² + 2(-1) + 1 =
0. Vértice
(-1, 0)
- f(x) = -x² + 4x – 3: x v = -4 / (2
- -1) = 2; y v = -(2)² + 4(2)
- 3 =
1. Vértice
(2, 1)
- f(x) = 2x²
6x + 4
x v = 6 / (2
- 2) = 1.5; y v = 2(1.5)²
- 6(1.5) + 4 = -0.
5. Vértice
(1.5, -0.5)
Tabela com Coordenadas do Vértice
| Função | Coordenadas do Vértice (xv, yv) |
|---|---|
| f(x) = x² + 2x + 1 | (-1, 0) |
| f(x) = -x² + 4x – 3 | (2, 1) |
| f(x) = 2x² – 6x + 4 | (1.5, -0.5) |
Concavidade da Parábola
A concavidade da parábola indica se ela se abre para cima ou para baixo. Essa característica é determinada exclusivamente pelo coeficiente ‘a’ da equação quadrática.
Determinação da Concavidade

Se a > 0, a parábola tem concavidade para cima, apresentando um ponto de mínimo no vértice. Se a < 0, a parábola tem concavidade para baixo, apresentando um ponto de máximo no vértice.
Parábolas com Concavidades Diferentes
Uma parábola com concavidade para cima tem seu vértice como ponto mínimo, e os valores da função crescem indefinidamente à medida que x se afasta do vértice em ambas as direções. Uma parábola com concavidade para baixo tem seu vértice como ponto máximo, e os valores da função decrescem indefinidamente à medida que x se afasta do vértice em ambas as direções.
Exemplos de Funções com Concavidades Diferentes
Concavidade para cima: f(x) = x² + 2x + 1 (a = 1 > 0). O vértice (-1, 0) é um ponto de mínimo. A parábola se abre para cima.
Concavidade para baixo: f(x) = -x² + 4x – 3 (a = -1 < 0). O vértice (2, 1) é um ponto de máximo. A parábola se abre para baixo.
Interseção com os Eixos
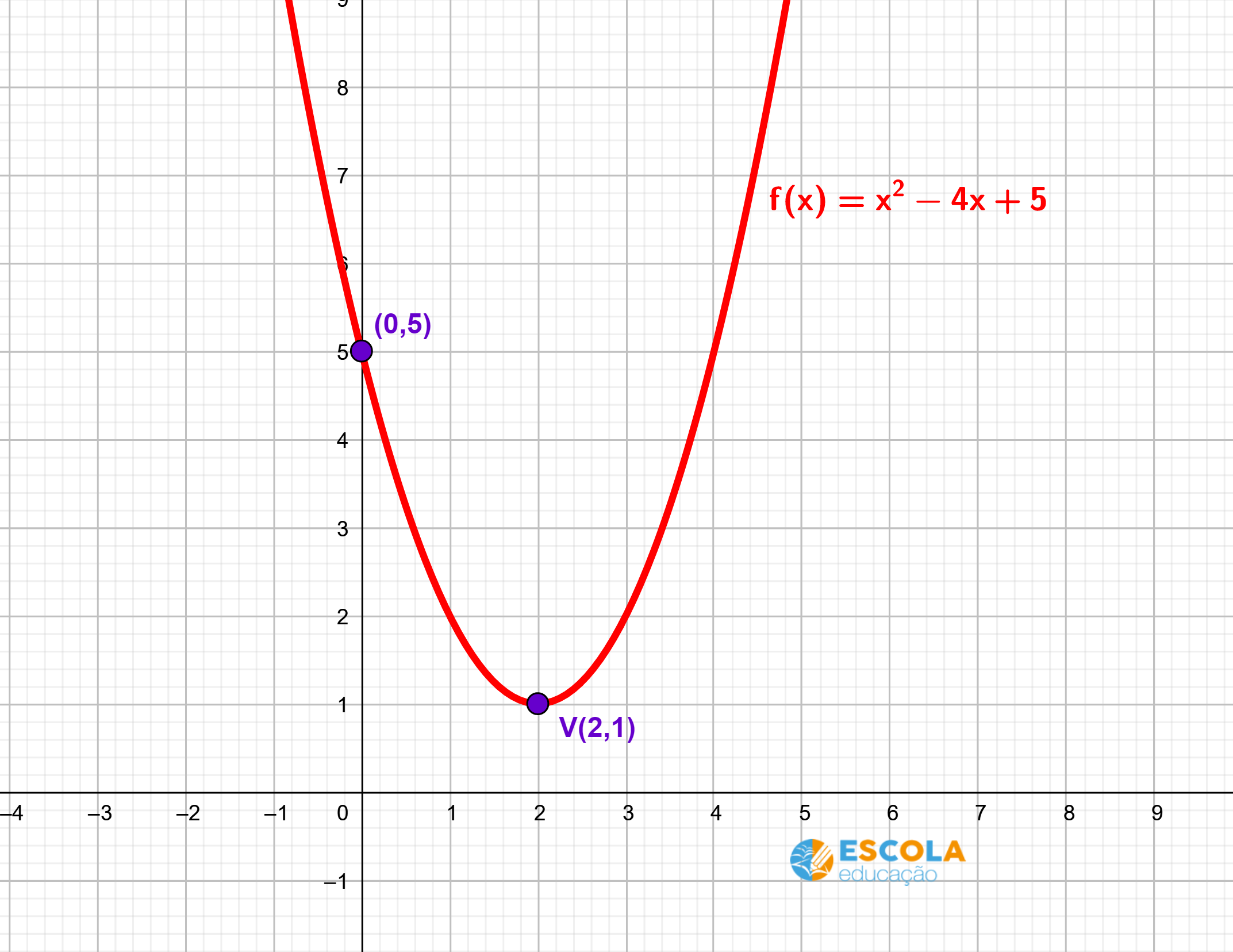
Determinar os pontos de interseção da parábola com os eixos x e y é fundamental para o esboço do gráfico.
Interseção com o Eixo x (Raízes), Exemplo De Função Do 2 Grau Exercicios Resolvidos Com Graficos
Os pontos de interseção com o eixo x são as raízes da função, encontradas através da resolução da equação ax² + bx + c = 0, utilizando métodos como a fórmula de Bhaskara ou a fatoração (já detalhados anteriormente).
Interseção com o Eixo y
O ponto de interseção com o eixo y é encontrado substituindo x = 0 na equação da função. Isso resulta em f(0) = c. Portanto, o ponto de interseção é (0, c).
- Substituir x = 0 na equação da função.
- Calcular o valor de f(0).
- O ponto de interseção com o eixo y é (0, f(0)).
Exemplos Numéricos
Exemplo 1 (Interseção com eixo x): f(x) = x²
-4. As raízes são x = 2 e x = -2 (resolvido pela fatoração ou Bhaskara).
Exemplo 2 (Interseção com eixo y): f(x) = 2x² + 3x – 1. A interseção com o eixo y é (0, -1) (f(0) = -1).
Construção do Gráfico
A construção do gráfico de uma função do 2º grau envolve a utilização das informações obtidas sobre as raízes, o vértice e a concavidade.
Guia Passo a Passo para Construção do Gráfico
- Determinar a concavidade da parábola (a > 0: concavidade para cima; a < 0: concavidade para baixo).
- Calcular as coordenadas do vértice (xv, y v).
- Encontrar as raízes (pontos de interseção com o eixo x), se existirem.
- Encontrar o ponto de interseção com o eixo y (0, c).
- Escolher alguns pontos adicionais para melhor precisão do gráfico, substituindo valores de x na equação e calculando os respectivos valores de y.
- Plotar os pontos encontrados no plano cartesiano.
- Desenhar a parábola, conectando os pontos e respeitando a concavidade.
Exemplo Completo
Vamos construir o gráfico de f(x) = x²
-2x – 3.
1. Concavidade: a = 1 > 0, portanto, concavidade para cima.
2. Vértice: x v = -(-2) / (2
– 1) = 1; y v = (1)²
-2(1)
-3 = –
4. Vértice: (1, -4).
3. Raízes: (x – 3)(x + 1) = 0 => x = 3 e x = -1.
4. Interseção com o eixo y: (0, -3).
5. Pontos adicionais: Para x = 2, y = -3; para x = -2, y = 5.
6. Descrição do gráfico: Uma parábola com concavidade para cima, vértice em (1, -4), interceptando o eixo x em (3, 0) e (-1, 0), e o eixo y em (0, -3). Passa pelos pontos (2, -3) e (-2, 5).
Aplicações da Função do 2º Grau
A função do 2º grau possui amplas aplicações em diversas áreas do conhecimento, modelando situações reais de forma eficaz.
Exemplos de Aplicações em Situações Reais
A função do 2º grau é utilizada para modelar trajetórias de projéteis na física, calcular áreas em geometria, descrever o crescimento ou decrescimento de populações em biologia, e otimizar processos em engenharia, entre outras aplicações.
Resolução de Problema Prático
Problema: Um foguete é lançado verticalmente para cima. Sua altura (em metros) em relação ao tempo (em segundos) é dada pela função h(t) = -5t² + 20t. Determine o tempo que o foguete leva para atingir a altura máxima e qual é essa altura máxima.
Resolução: A função h(t) é uma função quadrática com a = -5, b = 20, c =
0. O tempo para atingir a altura máxima corresponde à coordenada x do vértice: t v = -b / 2a = -20 / (2
– -5) = 2 segundos. A altura máxima corresponde à coordenada y do vértice: h(2) = -5(2)² + 20(2) = 20 metros.

