Determinantes: Uma Introdução: Determinantes Definição Exemplos Noção De Determinantes De Uma Matriz Quadrada
Determinantes Definição Exemplos Noção De Determinantes De Uma Matriz Quadrada – Determinantes são conceitos fundamentais na álgebra linear, associados a matrizes quadradas. Eles fornecem informações cruciais sobre as propriedades da matriz, sendo ferramentas essenciais em diversas áreas da matemática e suas aplicações. A compreensão do cálculo e das propriedades dos determinantes é vital para a resolução de sistemas de equações lineares, análise de transformações lineares e geometria analítica, entre outras aplicações.
A Noção de Determinante
O determinante de uma matriz quadrada é um número escalar que codifica informações importantes sobre a matriz. Sua existência e valor estão intrinsecamente ligados à invertibilidade da matriz: uma matriz quadrada é invertível se, e somente se, seu determinante é diferente de zero. Em termos mais simples, o determinante indica se uma transformação linear representada pela matriz é singular (não invertível) ou não-singular (invertível).
Uma transformação linear não-singular preserva dimensões e não “colapsa” o espaço vetorial. Determinantes também são utilizados para calcular áreas e volumes em geometria analítica.
Cálculo de Determinantes, Determinantes Definição Exemplos Noção De Determinantes De Uma Matriz Quadrada

O cálculo de determinantes varia de acordo com a ordem da matriz. Para matrizes de ordem baixa, o cálculo é direto. Para matrizes de ordem superior, métodos mais sofisticados, como a expansão por cofatores (método de Laplace), são necessários.
Determinantes de Matrizes 2×2 e 3×3
Para uma matriz 2×2,
| Matriz 2×2 | Determinante | Matriz 2×2 | Determinante |
|---|---|---|---|
| [[1, 2], [3, 4]] | (1*4) – (2*3) = -2 | [[-1, 0], [2, 5]] | (-1*5) – (0*2) = -5 |
| [[0, 1], [-1, 0]] | (0*0) – (1*-1) = 1 | [[2, -3], [4, 1]] | (2*1) – (-3*4) = 14 |
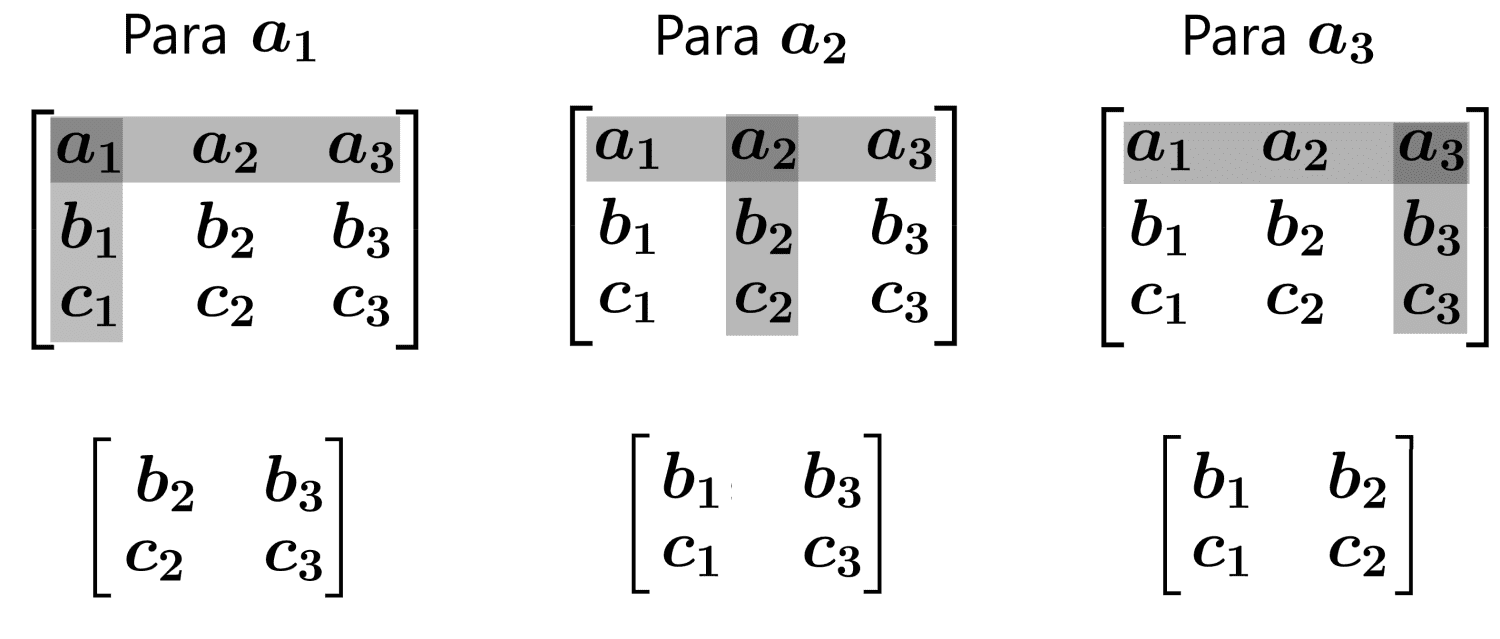
Método de Laplace (Expansão por Cofatores)
Para matrizes de ordem superior a 3, o método de Laplace é uma técnica eficiente. Ele envolve expandir o determinante ao longo de uma linha ou coluna, utilizando os cofatores dos elementos.
- Escolha uma linha ou coluna da matriz.
- Para cada elemento da linha ou coluna escolhida, calcule seu cofator, que é o determinante da submatriz obtida ao remover a linha e a coluna do elemento, multiplicado por (-1)^(i+j), onde i e j são os índices da linha e coluna do elemento.
- Multiplique cada elemento da linha ou coluna escolhida pelo seu cofator.
- Some os resultados obtidos no passo anterior. A soma é o determinante da matriz.
Exemplo: Considere uma matriz 4×4. A expansão por cofatores ao longo da primeira linha envolveria calcular quatro determinantes 3×3, cada um multiplicado pelo respectivo elemento da primeira linha e pelo fator (-1)^(1+j).
Propriedades dos Determinantes
Os determinantes possuem diversas propriedades que simplificam seu cálculo. Essas propriedades são úteis para reduzir a complexidade computacional e explorar a estrutura da matriz.
| Propriedade | Descrição |
|---|---|
| Determinante da matriz transposta | O determinante de uma matriz é igual ao determinante de sua transposta: det(AT) = det(A). |
| Determinante do produto de matrizes | O determinante do produto de duas matrizes é o produto dos determinantes: det(AB) = det(A)det(B). |
| Determinante de uma matriz triangular | O determinante de uma matriz triangular (superior ou inferior) é o produto dos elementos da diagonal principal. |
| Efeito da multiplicação de uma linha/coluna por um escalar | Se uma linha ou coluna de uma matriz é multiplicada por um escalar k, o determinante é multiplicado por k. |
| Efeito da troca de duas linhas/colunas | Se duas linhas ou colunas de uma matriz são trocadas, o determinante muda de sinal. |
Aplicações dos Determinantes
Os determinantes têm aplicações práticas em diversas áreas, como a geometria analítica e a resolução de sistemas de equações lineares. Sua capacidade de fornecer informações sobre a invertibilidade de matrizes e as propriedades geométricas de transformações lineares os torna ferramentas poderosas.
Cálculo de Áreas e Volumes
Em geometria analítica, o determinante pode ser usado para calcular a área de um paralelogramo ou o volume de um paralelepípedo. Considere dois vetores
Determinantes e Sistemas Lineares
A relação entre determinantes e sistemas de equações lineares é fundamental. O determinante da matriz de coeficientes indica se o sistema possui uma única solução, infinitas soluções ou nenhuma solução.
Regra de Cramer
A Regra de Cramer é um método para resolver sistemas de equações lineares que utiliza determinantes. Para um sistema de n equações com n incógnitas, se o determinante da matriz de coeficientes é diferente de zero, então o sistema possui uma única solução, que pode ser calculada usando a regra de Cramer. Cada incógnita é calculada como a razão entre o determinante de uma matriz modificada (onde uma coluna da matriz de coeficientes é substituída pelo vetor dos termos constantes) e o determinante da matriz de coeficientes original.
Exemplo: Considere o sistema 2x + y = 5 e x – 2y = -4. A matriz de coeficientes é [[2, 1], [1, -2]]. O determinante é (2*-2)
-(1*1) = -5. Como o determinante é diferente de zero, o sistema possui uma única solução, que pode ser calculada usando a regra de Cramer.
Exemplos Avançados de Determinantes
Matrizes triangulares e matrizes com muitos zeros simplificam o cálculo de determinantes. Em matrizes triangulares, o determinante é simplesmente o produto dos elementos da diagonal principal. Matrizes com muitos zeros podem ser simplificadas usando operações elementares de linhas e colunas para reduzir o número de cálculos necessários. Para matrizes de ordem superior (4×4 e 5×5), a expansão por cofatores, combinada com estratégias para escolher linhas ou colunas com o maior número de zeros, pode tornar o processo mais eficiente.
Exemplo: Uma matriz triangular superior 4×4 terá seu determinante como o produto dos elementos da diagonal principal. Uma matriz 5×5 com muitos zeros pode ser simplificada através de operações elementares de linhas para obter uma matriz com mais zeros, facilitando a expansão por cofatores.
Concluindo nossa exploração do universo dos determinantes, fica claro seu papel central na álgebra linear e em diversas áreas aplicadas. De sua definição concisa à sua aplicação em problemas complexos, compreendemos sua importância na resolução de sistemas de equações, na análise da invertibilidade de matrizes e em diversas outras aplicações práticas. Dominar o cálculo de determinantes, seja em matrizes 2×2, 3×3 ou de ordem superior, utilizando métodos como a regra de Laplace, é essencial para qualquer profissional que lide com modelagem matemática.
Aprofundar o conhecimento sobre as propriedades dos determinantes, por sua vez, permite simplificações e otimizações no cálculo, tornando o processo mais eficiente e menos propenso a erros. A jornada pelo mundo dos determinantes não termina aqui; ela serve como um ponto de partida para explorações mais profundas em áreas como álgebra linear avançada e suas aplicações em campos científicos e tecnológicos.

