Frações Equivalentes: Uma Exploração Detalhada: 4. Explique O Que São Frações Equivalentes. Dê Dois Exemplos.
. Explique O Que São Frações Equivalentes. Dê Dois Exemplos. – Frações equivalentes representam a mesma parte de um todo, mesmo que sejam escritas de forma diferente. Compreender o conceito de frações equivalentes é fundamental para o domínio da aritmética e para a resolução de problemas matemáticos em diversas áreas, desde o cálculo de porcentagens até a compreensão de proporções em situações cotidianas.
Introdução ao Conceito de Frações Equivalentes, 4. Explique O Que São Frações Equivalentes. Dê Dois Exemplos.
Frações equivalentes são frações que representam a mesma quantidade, embora seus numeradores e denominadores sejam diferentes. A relação entre o numerador e o denominador em frações equivalentes é que a razão entre eles permanece constante. Em outras palavras, se multiplicarmos ou dividirmos o numerador e o denominador de uma fração por um mesmo número (diferente de zero), obteremos uma fração equivalente.
Imagine uma pizza dividida em 4 fatias iguais. Se você comer 2 fatias, comeu 2/4 da pizza. Agora, imagine a mesma pizza dividida em 8 fatias iguais. Se você comer 4 fatias, também comeu 2/4 (ou 1/2) da pizza. Tanto 2/4 quanto 4/8 representam a mesma porção da pizza, sendo, portanto, frações equivalentes.
| Fração | Representação Visual (Pizza) | Representação Visual (Barra de Chocolate) | Representação Visual (Gráfico) |
|---|---|---|---|
| 1/2 | Metade de uma pizza dividida em duas partes iguais. | Metade de uma barra de chocolate dividida em duas partes iguais. | Um gráfico circular com metade pintada. |
| 2/4 | Duas fatias de uma pizza dividida em quatro partes iguais. | Duas partes de uma barra de chocolate dividida em quatro partes iguais. | Um gráfico circular com duas de quatro partes pintadas. |
| 3/6 | Três fatias de uma pizza dividida em seis partes iguais. | Três partes de uma barra de chocolate dividida em seis partes iguais. | Um gráfico circular com três de seis partes pintadas. |
| 4/8 | Quatro fatias de uma pizza dividida em oito partes iguais. | Quatro partes de uma barra de chocolate dividida em oito partes iguais. | Um gráfico circular com quatro de oito partes pintadas. |
Multiplicação e Divisão para Encontrar Frações Equivalentes
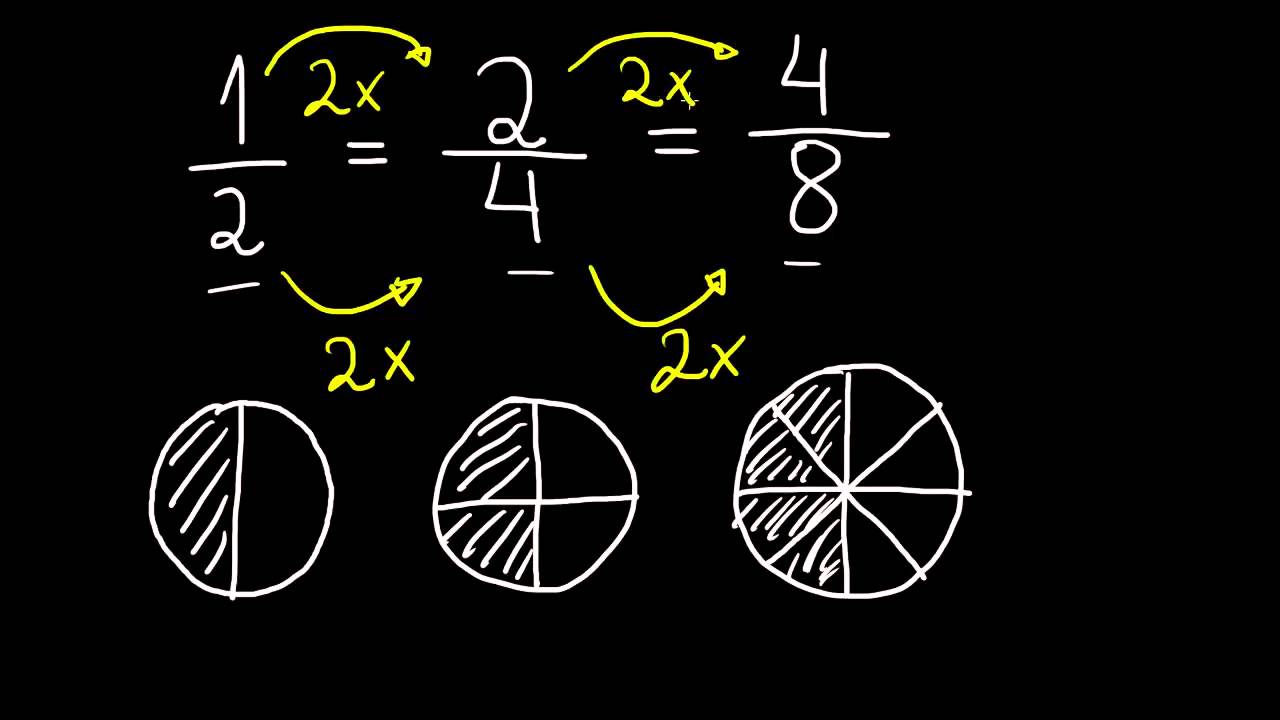
Existem dois métodos principais para encontrar frações equivalentes: multiplicação e divisão. Ambos os métodos envolvem a multiplicação ou divisão do numerador e do denominador por um mesmo número, mantendo a proporção entre eles.
- Multiplicação: Para obter uma fração equivalente maior, multiplicamos o numerador e o denominador por um mesmo número inteiro. Exemplo: 1/2 x 2/2 = 2/
4. Outro exemplo: 3/5 x 4/4 = 12/20. - Divisão: Para obter uma fração equivalente menor (simplificação), dividimos o numerador e o denominador por um mesmo número inteiro (o maior divisor comum). Exemplo: 6/9 ÷ 3/3 = 2/
3. Outro exemplo: 12/16 ÷ 4/4 = 3/4.
A similaridade entre os métodos é que ambos preservam a proporção da fração original. A diferença está no resultado: a multiplicação gera frações maiores, enquanto a divisão gera frações menores.
Simplificação de Frações
Uma fração irredutível é uma fração que não pode ser simplificada, ou seja, o numerador e o denominador não possuem nenhum divisor comum maior que 1. A simplificação de frações até sua forma irredutível envolve encontrar o máximo divisor comum (MDC) entre o numerador e o denominador e dividir ambos por esse número.
Para encontrar o MDC, podemos utilizar a fatoração em números primos ou o método da subtração sucessiva. Por exemplo, para simplificar a fração 12/18, encontramos o MDC(12,18) = 6. Dividindo o numerador e o denominador por 6, obtemos a fração irredutível 2/3.
Exemplo mais complexo: Simplifique 24/36. Fatorando 24 = 2³ x 3 e 36 = 2² x 3², o MDC é 2² x 3 = 12. Então, 24/36 ÷ 12/12 = 2/3.
Exemplos de Frações Equivalentes
Aqui estão dois exemplos de frações equivalentes, mostrando o processo de obtenção:
| Fração Original | Fração Equivalente | Cálculo |
|---|---|---|
| 1/3 | 4/12 | 1/3 x 4/4 = 4/12 |
| 2/5 | 6/15 | 2/5 x 3/3 = 6/15 |
A fração 5/7 não pode ser simplificada porque o MDC(5,7) = 1.
Aplicação de Frações Equivalentes em Problemas
Imagine que você tem uma receita que pede 1/2 xícara de açúcar, mas você só tem uma xícara de medida de 1/4. Usando frações equivalentes, você pode descobrir que precisa de duas medidas de 1/4 de xícara de açúcar (1/2 = 2/4).
Outro exemplo: Uma loja oferece desconto de 1/3 em todos os produtos. Se um produto custa R$ 60,00, qual o valor do desconto? 1/3 de 60 = (1/3) x 60/1 = 20. O desconto é de R$ 20,00.
Como saber se duas frações são equivalentes?
Simplifique ambas as frações até a forma irredutível. Se chegarem na mesma fração irredutível, elas são equivalentes.
Qual a utilidade das frações equivalentes no dia a dia?
São úteis em diversas situações, como dividir alimentos, calcular porcentagens, comparar quantidades e resolver problemas de proporção.
Existe um limite de frações equivalentes para uma fração dada?
Não, existem infinitas frações equivalentes para qualquer fração, exceto para 0/n (onde n é um número diferente de zero).

